Skip to main content

Week 03

About 4 min

Week 03 관련

REALTIVISTICI MASS

m=γ m0,<m0: mass at rest> \begin{align*} m&=\gamma\:m_0,&\left<m_0:\:\text{mass at rest}\right> \end{align*}

in NON-RELATIVISTIC frame (PHYS031)

E=W=∫F⃗⋅dx⃗=∫(ma⃗)⋅dx⃗=∫m(dv⃗dt)⋅x⃗=∫m(dx⃗dt)dv⃗=∫m(v)(dv)=m(v22)=12mv2; \begin{align*} E&=W=\int{\vec{F}\cdot{d}\vec{x}}=\int{\left(m\vec{a}\right)\cdot{d}\vec{x}}\\ &=\int{m\left(\frac{d\vec{v}}{dt}\right)\cdot\vec{x}}=\int{m\left(\frac{d\vec{x}}{dt}\right)d\vec{v}}\\ &=\int{m(v)(dv)}=m\left(\frac{v^2}{2}\right)=\frac{1}{2}mv^2; \end{align*}

in RELATIVISTIC frame

E=W=∫F⃗⋅dx⃗=∫(dpdt)dx,<F=dpdt>=∫ddt(p)dx=∫ddt(γm0v)=∫m0(γdvdt+vdγdt)=⋯ \begin{align*} E&=W=\int{\vec{F}\cdot{d}\vec{x}}=\int{\left(\frac{dp}{dt}\right)dx},&&\left<F=\frac{dp}{dt}\right>\\ &=\int{\frac{d}{dt}(p)dx}=\int{\frac{d}{dt}\left(\gamma{m_0}v\right)}\\ &=\int{m_0\left(\gamma\frac{dv}{dt}+v\frac{d\gamma}{dt}\right)}\\ &=\cdots \end{align*}

{γ=(1−v2c2)−12;dγdt=ddt(γ)=ddt(1−v2c2)−12=(−12)(1−v2c2)−32[(−2vc2)(dvdt)]=vc2γ3dvdt} \left\{ \begin{align*} \gamma&=\left(1-\frac{v^2}{c^2}\right)^{-\frac{1}{2}};\\ \frac{d\gamma}{dt}&=\frac{d}{dt}\left(\gamma\right)=\frac{d}{dt}\left(1-\frac{v^2}{c^2}\right)^{-\frac{1}{2}}\\ &=\left(-\frac{1}{2}\right)\left(1-\frac{v^2}{c^2}\right)^{-\frac{3}{2}}\left[\left(-\frac{2v}{c^2}\right)\left(\frac{dv}{dt}\right)\right]\\ &=\frac{v}{c^2}\gamma^3\frac{dv}{dt} \end{align*} \right\}

E=∫m0(γdvdt+v(vc2γ3dvdt))dx=∫m0(γdv+v2c2γ3dv)dxdt=∫m0γdv(1+v2c2γ2)dxdt \begin{align*} E&=\int{m_0\left(\gamma\frac{dv}{dt}+v\left(\frac{v}{c^2}\gamma^3\frac{dv}{dt}\right)\right)dx}\\&=\int{m_0\left(\gamma{dv}+\frac{v^2}{c^2}\gamma^3dv\right)\frac{dx}{dt}}=\int{m_0\gamma{dv}\left(1+\frac{v^2}{c^2}\gamma^2\right)\frac{dx}{dt}} \end{align*}

{1+v2c2γ2=1+(v2c2)(c2c2−v2)=1+v2c2−v2=(v2c2−v2)+(c2−v2c2−v2)=c2c2−v2=γ2} \left\{ \begin{align*} 1+\frac{v^2}{c^2}\gamma^2&=1+\left(\frac{v^2}{c^2}\right)\left(\frac{c^2}{c^2-v^2}\right)=1+\frac{v^2}{c^2-v^2}\\ &=\left(\frac{v^2}{c^2-v^2}\right)+\left(\frac{c^2-v^2}{c^2-v^2}\right)=\frac{c^2}{c^2-v^2}=\gamma^2 \end{align*} \right\}

E=∫m0γ(γ2)dv(v)=∫m0γ3v dv,<dγdt=vc2γ3dvdt;    dγ=vc2γ3dv>=∫m0(c2)dγ=m0c2∫dγ=γm0c2; \begin{align*} E&=\int{m_0\gamma(\gamma^2)dv(v)}=\int{m_0\gamma^3v\:dv},\\ &\left<\frac{d\gamma}{dt}=\frac{v}{c^2}\gamma^3\frac{dv}{dt};\:\:\:\:d\gamma=\frac{v}{c^2}\gamma^3dv\right>\\ &=\int{m_0(c^2)d\gamma}=m_0c^2\int{d\gamma}=\gamma{m_0}c^2; \end{align*}

∴E=γm0c2 \begin{align*} \therefore{E}&=\gamma{m_0}c^2 \end{align*}

Give the lower and upper bounds for this integral

E=m0c2(1−v2c2)−12∣0v=m0c2(1−(v)2c2)−12−m0c2(1−(0)2c2)−12=m0c2γ−m0c2=(γ−1)m0c2; \begin{align*} E&=m_0c^2\left.\left(1-\frac{v^2}{c^2}\right)^{-\frac{1}{2}}\right|_{0}^v\\ &=m_0c^2\left(1-\frac{(v)^2}{c^2}\right)^{-\frac{1}{2}}-m_0c^2\left(1-\frac{(0)^2}{c^2}\right)^{-\frac{1}{2}}\\ &=m_0c^2\gamma-m_0c^2=(\gamma-1)m_0c^2; \end{align*}

given velocity "close" to speed of light, the kinetic energy is denoted,

K=γm0c2−m0c2=Etotal−Erest=(γ−1)m0c2 \begin{align*} K&=\gamma{m_0}c^2-m_0c^2=E_{\text{total}}-E_{\text{rest}}\\ &=(\gamma-1)m_0c^2 \end{align*}

to see if this equation holds true in classical physics.

{v≪c,γ≈1+12v2c2Binomial Expansion} \left\{ \begin{align*} v\ll{c},&\underset{\text{Binomial Expansion}}{\gamma\approx1+\frac{1}{2}\frac{v^2}{c^2}} \end{align*}\right\}

K≈[(1+12v2c2)−1]m0c2=12m0v2 \begin{align*} K\approx\left[\left(1+\frac{1}{2}\frac{v^2}{c^2}\right)-1\right]m_0c^2=\frac{1}{2}m_0v^2 \end{align*}

ENERGY RELATION ($$E_{\text{total}} vs. E_{\text{rest}}$$)

m=γm0;m2=γ2m02=(c2c2−v2)m02;m02c2=m2(c2−v2)=m2c2−m2v2;(m02c2)(c2)=(c2)(m2c2−m2v2);(m0c2)2=(mc2)2−m2c2v2;(mc2)2=m2c2v2+(m0c2)2;<E=m0c2>    <p=mv>(Etotal)2=(pc)2+(Erest)2 \begin{align*} m&=\gamma{m_0};\\ m^2&=\gamma^2m_0^2=\left(\frac{c^2}{c^2-v^2}\right)m_0^2;\\ m_0^2c^2&=m^2(c^2-v^2)=m^2c^2-m^2v^2;\\ (m_0^2c^2)(c^2)&=(c^2)(m^2c^2-m^2v^2);\\ (m_0c^2)^2&=(mc^2)^2-m^2c^2v^2;\\ (mc^2)^2&=m^2c^2v^2+(m_0c^2)^2;\\ &\left<E=m_0c^2\right>\:\:\:\:\left<p=mv\right>\\ (E_{\text{total}})^2&=(pc)^2+(E_{\text{rest}})^2 \end{align*}

DIREC'S DISCOVERY

Basically he proposed that in special relativity, electrons can have both a positive charge and negative energy.

Q: how is it possible to have an electron with energy that is positively charged?

PARTICLE COLLISION

RELATIONSHIP BETWEEN ENERGY & MASS

E=mc3 E=mc^3

SLIDES:

pˉ+p→many \bar{p}+p\to{\text{many}}

PROTON & NEUTRON

proton:

mp=938.3 MeV/c2 m_p=938.3\:\text{MeV}/c^2

neutron:

mn=939.6 MeV/c2 m_n=939.6\:\text{MeV}/c^2

deutreon:

md=(mp+mn)=(939.6+939.6)=1877.05 MeV/c2 \begin{align*} m_d&=(m_p+m_n)\\ &=(939.6+939.6)\\ &=1877.05\:\text{MeV}/c^2 \end{align*}

Q: But from the investigation, this is simply shown not true. Will it be larger or smaller?

A: it is LESS .

md=1875.6 MeV/c2 m_d=1875.6\:\text{MeV}/c^2

What happened? See here.

QUANTUM PHYSICS: DISCOVERY

1792

Thomas Wedgwood

  • pioneer of photography.
  • We used to work for pottery shop owned by his dad, Josiah Wedgwood.
  • Discovery: Regardless of shape, thing glowed in the same colord and at the same temperature (generally high).

Kirchoff

  • spectroradiancy

EA∝RT(f);<RT(f)power flux=1[Wm2⋅1f]=[]1f> \frac{E}{A}\propto{R_T}(f);\\ \begin{align*} \left<\underset{\text{power flux}}{R_T(f)}=1\left[\frac{\text{W}}{\text{m}^2}\cdot\frac{1}{f}\right]=\left[\right]\frac{1}{f}\right> \end{align*}

  • black body
    • black body tends to absorb more heat.
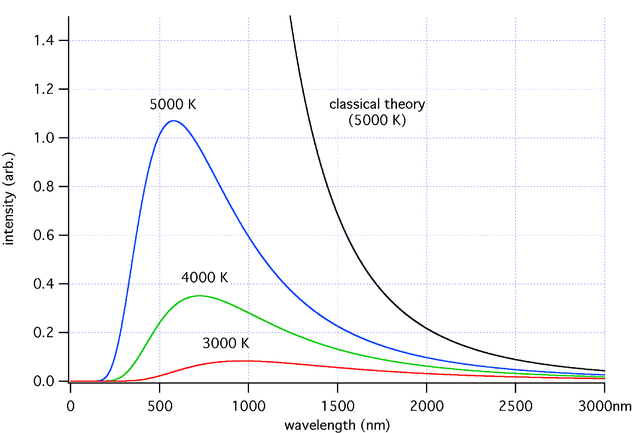black body radiation graph
black body radiation graph

<RT(f)power flux=1[Wm2⋅1f]> \begin{align*} \left<\underset{\text{power flux}}{R_T(f)}=1\left[\frac{\text{W}}{\text{m}^2}\cdot\frac{1}{f}\right]\right> \end{align*}

RT(f)=Et⋅A⋅1f=Et⋅(Lvol)⋅1f=Evol⋅Lt⋅1f=(ρT(t))energy density(v)(1f)∴RT(f)∝(ρT(t))⋅1f \begin{align*} R_T(f)&=\frac{E}{t\cdot{A}}\cdot\frac{1}{f}\\ &=\frac{E}{t}\cdot\left(\frac{L}{\text{vol}}\right)\cdot\frac{1}{f}\\ &=\frac{E}{\text{vol}}\cdot\frac{L}{\text{t}}\cdot\frac{1}{f}\\ &=\underset{\text{energy density}}{\left(\rho_T(t)\right)}\left(v\right)\left(\frac{1}{f}\right)\\ \therefore{R}_T(f)&\propto\left(\rho_T(t)\right)\cdot\frac{1}{f} \end{align*}

INTERFERENCE

standing waves (1-D)

y1=A sin⁡(kx+ωt)y2=A sin⁡(kx−ωt) \begin{align*} y_1&=A\:\sin{(kx+\omega{t})}\\ y_2&=A\:\sin{(kx-\omega{t})} \end{align*}

{y=Asin⁡ϕ‾ϕ=kx‾+ω t,<k:wave #>kx=d±ω tx=dk±ωkt,<v=ωk>=C±v t;} \left\{ \begin{align*} y&=A\sin{\underline{\phi}}\\ \phi&=\underline{kx}+\omega\:t,&&\left<k:\text{wave }\#\right>\\ kx&=d\pm\omega\:t\\ x&=\frac{d}{k}\pm\frac{\omega}{k}t,&&\left<v=\frac{\omega}{k}\right>\\ &=C\pm{v}\:t; \end{align*} \right\}

y1+y2=Asin⁡(kx+ωt)+Asin⁡(kx−ωt)<sin⁡(a)+sin⁡(b)=2[sin⁡(12(a+b))cos⁡(12(a−b))]>=2Asin⁡((kx+ωt)+(kx−ωt)2)cos⁡((kx+ωt)−(kx−ωt)2)=2Asin⁡(kx)cos⁡(ωt) \begin{align*} y_1+y_2&=A\sin{(kx+\omega{t})}+A\sin{(kx-\omega{t})}\\ &\left<\sin{(a)}+\sin{(b)}=2\left[\sin{\left(\frac{1}{2}(a+b)\right)}\cos{\left(\frac{1}{2}(a-b)\right)}\right]\right>\\ &=2A\sin{\left(\frac{(kx+\omega{t})+(kx-\omega{t})}{2}\right)}\cos{\left(\frac{(kx+\omega{t})-(kx-\omega{t})}{2}\right)}\\ &=2A\sin{(kx)}\cos{(\omega{t})} \end{align*}

{kx=nπ;(2πλ)L=nπ;λ=2Ln;} \left\{ \begin{align*} kx&=n\pi;\\ \left(\frac{2\pi}{\lambda}\right)L&=n\pi;\\ \lambda&=\frac{2L}{n}; \end{align*} \right\}

vibration of standing wave

f=vλ=(n2L)v=nv2Lfc=(c2L)nEM Wave (1D);fc=(c2L)(nx)2+(ny)2+(nz)2EM Wave (3D);<n:mode #L:size of capacity> \begin{align*} f&=\frac{v}{\lambda}=\left(\frac{n}{2L}\right)v=\frac{nv}{2L}\\ f_{c}&\underset{\text{EM Wave (1D)}}{=\left(\frac{c}{2L}\right)n};\\ f_{c}&\underset{\text{EM Wave (3D)}}{=\left(\frac{c}{2L}\right)\sqrt{(n_x)^2+(n_y)^2+(n_z)^2}};\\ &\left<\begin{matrix}n:\text{mode \#}&&L:\text{size of capacity}\end{matrix}\right> \end{align*}

For EM wave

BLAKC BODY

https://en.m.wikipedia.org/wiki/Black_body