The Insertion Sort Algorithm in Python

Santiago ValdarramaApril 15, 2020About 5 min

The Insertion Sort Algorithm in Python 관련

In this tutorial, you'll learn all about five different sorting algorithms in Python from both a theoretical and a practical standpoint. You'll also learn several related and important concepts, including Big O notation and recursion.

Sorting Algorithms in Python

Like bubble sort, the insertion sort algorithm is straightforward to implement and understand. But unlike bubble sort, it builds the sorted list one element at a time by comparing each item with the rest of the list and inserting it into its correct position. This “insertion” procedure gives the algorithm its name.

An excellent analogy to explain insertion sort is the way you would sort a deck of cards. Imagine that you’re holding a group of cards in your hands, and you want to arrange them in order. You’d start by comparing a single card step by step with the rest of the cards until you find its correct position. At that point, you’d insert the card in the correct location and start over with a new card, repeating until all the cards in your hand were sorted.

Implementing Insertion Sort in Python

The insertion sort algorithm works exactly like the example with the deck of cards. Here’s the implementation in Python:

def insertion_sort(array):
    # Loop from the second element of the array until
    # the last element
    for i in range(1, len(array)):
        # This is the element we want to position in its
        # correct place
        key_item = array[i]

        # Initialize the variable that will be used to
        # find the correct position of the element referenced
        # by `key_item`
        j = i - 1

        # Run through the list of items (the left
        # portion of the array) and find the correct position
        # of the element referenced by `key_item`. Do this only
        # if `key_item` is smaller than its adjacent values.
        while j >= 0 and array[j] > key_item:
            # Shift the value one position to the left
            # and reposition j to point to the next element
            # (from right to left)
            array[j + 1] = array[j]
            j -= 1

        # When you finish shifting the elements, you can position
        # `key_item` in its correct location
        array[j + 1] = key_item

    return array

Unlike bubble sort, this implementation of insertion sort constructs the sorted list by pushing smaller items to the left. Let’s break down insertion_sort() line by line:

Line 4 sets up the loop that determines the key_item that the function will position during each iteration. Notice that the loop starts with the second item on the list and goes all the way to the last item.
Line 7 initializes key_item with the item that the function is trying to place.
Line 12 initializes a variable that will consecutively point to each element to the left of key item. These are the elements that will be consecutively compared with key_item.
Line 18 compares key_item with each value to its left using a while loop, shifting the elements to make room to place key_item.
Line 27 positions key_item in its correct place after the algorithm shifts all the larger values to the right.

Here’s a figure illustrating the different iterations of the algorithm when sorting the array [8, 2, 6, 4, 5]:

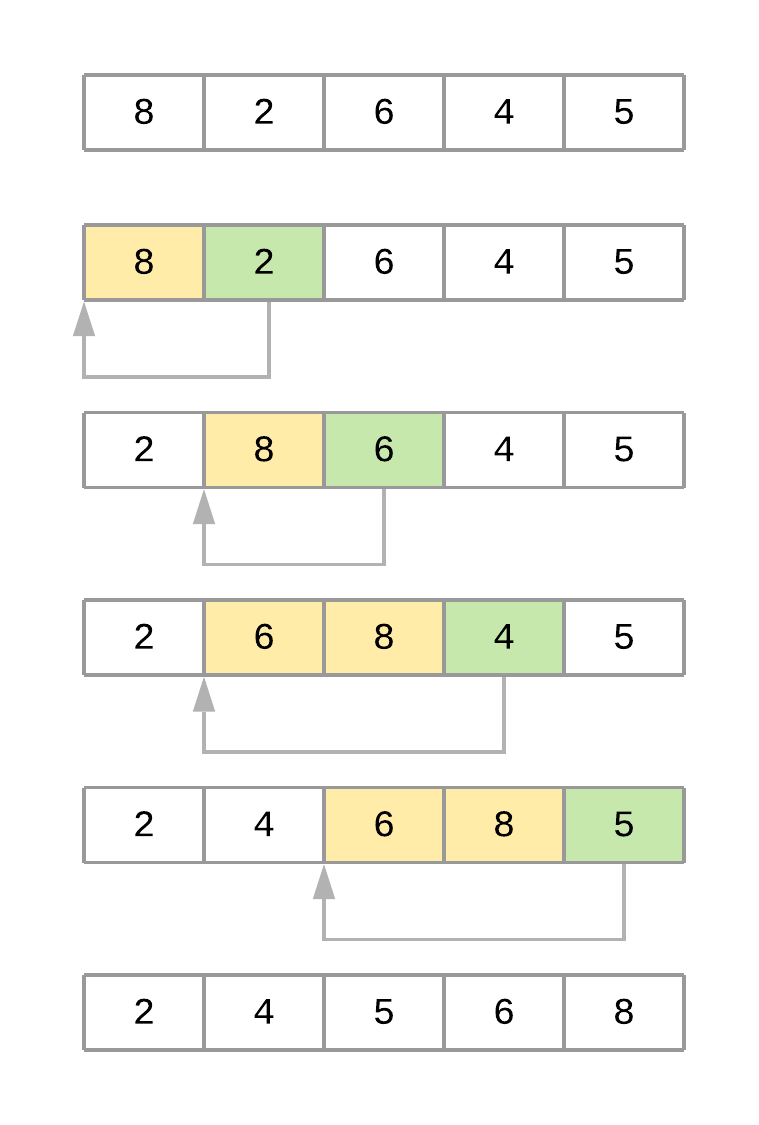
The Insertion Sort Process

Now here’s a summary of the steps of the algorithm when sorting the array:

The algorithm starts with key_item = 2 and goes through the subarray to its left to find the correct position for it. In this case, the subarray is [8].
Since $2\gt8$ , the algorithm shifts element 8 one position to its right. The resultant array at this point is [8, 8, 6, 4, 5].
Since there are no more elements in the subarray, the key_item is now placed in its new position, and the final array is [2, 8, 6, 4, 5].
The second pass starts with key_item = 6 and goes through the subarray located to its left, in this case [2, 8].
Since $6\gt8$ , the algorithm shifts 8 to its right. The resultant array at this point is [2, 8, 8, 4, 5].
Since $6\lt2$ , the algorithm doesn’t need to keep going through the subarray, so it positions key_item and finishes the second pass. At this time, the resultant array is [2, 6, 8, 4, 5].
The third pass through the list puts the element 4 in its correct position, and the fourth pass places element 5 in the correct spot, leaving the array sorted.

Measuring Insertion Sort’s Big O Runtime Complexity

Similar to your bubble sort implementation, the insertion sort algorithm has a couple of nested loops that go over the list. The inner loop is pretty efficient because it only goes through the list until it finds the correct position of an element. That said, the algorithm still has an $O\left(n^{2}\right)$ runtime complexity on the average case.

The worst case happens when the supplied array is sorted in reverse order. In this case, the inner loop has to execute every comparison to put every element in its correct position. This still gives you an $O\left(n^{2}\right)$ runtime complexity.

The best case happens when the supplied array is already sorted. Here, the inner loop is never executed, resulting in an $O\left(n\right)$ runtime complexity, just like the best case of bubble sort.

Although bubble sort and insertion sort have the same Big O runtime complexity, in practice, insertion sort is considerably more efficient than bubble sort. If you look at the implementation of both algorithms, then you can see how insertion sort has to make fewer comparisons to sort the list.

Timing Your Insertion Sort Implementation

To prove the assertion that insertion sort is more efficient than bubble sort, you can time the insertion sort algorithm and compare it with the results of bubble sort. To do this, you just need to replace the call to run_sorting_algorithm() with the name of your insertion sort implementation:

if __name__ == "__main__":
    # Generate an array of `ARRAY_LENGTH` items consisting
    # of random integer values between 0 and 999
    array = [randint(0, 1000) for i in range(ARRAY_LENGTH)]

    # Call the function using the name of the sorting algorithm
    # and the array we just created
    run_sorting_algorithm(algorithm="insertion_sort", array=array)

You can execute the script as before:

python sorting.py
# 
# Algorithm: insertion_sort. Minimum execution time: 56.71029764299999

Notice how the insertion sort implementation took around 17 fewer seconds than the bubble sort implementation to sort the same array. Even though they’re both $O\left(n^{2}\right)$ algorithms, insertion sort is more efficient.

Analyzing the Strengths and Weaknesses of Insertion Sort

Just like bubble sort, the insertion sort algorithm is very uncomplicated to implement. Even though insertion sort is an $O\left(n^{2}\right)$ algorithm, it’s also much more efficient in practice than other quadratic implementations such as bubble sort.

There are more powerful algorithms, including merge sort and Quicksort, but these implementations are recursive and usually fail to beat insertion sort when working on small lists. Some Quicksort implementations even use insertion sort internally if the list is small enough to provide a faster overall implementation. Timsort also uses insertion sort internally to sort small portions of the input array.

That said, insertion sort is not practical for large arrays, opening the door to algorithms that can scale in more efficient ways.