Enhancing Digital Signatures: The Transition to PSS

Hamdaan AliApril 3, 2025About 5 min

Enhancing Digital Signatures: The Transition to PSS 관련

The Cryptography Handbook: Exploring RSA PKCSv1.5, OAEP, and PSS

The RSA algorithm was introduced in 1978 in the seminal paper, ”A Method for Obtaining Digital Signatures and Public-Key Cryptosystems”. Over the decades, as RSA became integral to secure communications, various vulnerabilities and attacks have emerg...

The Cryptography Handbook: Exploring RSA PKCSv1.5, OAEP, and PSS

Now that you understand how OAEP transformed RSA encryption by mitigating vulnerabilities in deterministic padding, it’s time to turn our attention to RSA digital signatures – a critical function for ensuring message integrity and authenticity.

Early RSA signature schemes suffered from similar problems as raw encryption: their deterministic nature made them prone to forgery and replay attacks. This vulnerability paved the way for an improvement: the Probabilistic Signature Scheme (PSS).

Before we dive into PSS itself, let’s quickly understand the pain points with early RSA signatures.

Problems with Early RSA Signature Schemes

Traditional RSA signatures were generated by simply applying the RSA decryption function on a message digest (often with minimal formatting):

s=m^{d}\:\text{mod}\:N

where m is the hash (or encoded hash) of the message. This approach was deterministic which meant that each time the same message was signed, the exact signature was produced. Such determinism had two major drawbacks:

1. Predictability and Replay

Since the signature for a given message was always identical, an attacker could replay a captured signature with impunity or forge signatures if they could deduce patterns in the signature scheme.

2. Forgery Risks

In a deterministic setting, if an attacker finds any structure or mathematical relationship in the signature, they might be able to forge a valid signature for a new message. In certain scenarios, weak formatting could allow an adversary to create a “signature transformation” that produces a valid signature without having access to the private key.

These issues highlighted that a signature scheme must be probabilistic to be secure against adaptive forgery attempts and to ensure non-repudiation. This means that the signer should not be able to repudiate a signature because it is bound to a random value known only at signing time.

Birth of the Probabilistic Signature Scheme (PSS)

Towards the end of 1998, Bellare and Rogaway also proposed a scheme to overcome the inherent limitations of deterministic RSA signatures^[1]. The core idea was to introduce randomness into the signature generation process so that even when signing the same message twice, the resulting signatures would be different. This randomness comes from a salt value and a carefully designed encoding process. The result is a signature method with strong, provable security guarantees.

This randomness prevents attackers from exploiting patterns in the signature process. The probabilistic Signature Scheme was designed to be provably secure in the random oracle model, meaning that forging a signature would be as hard as breaking RSA itself under certain assumptions^[2].

The block diagram below is a visual representation of the PSS encoding schema:

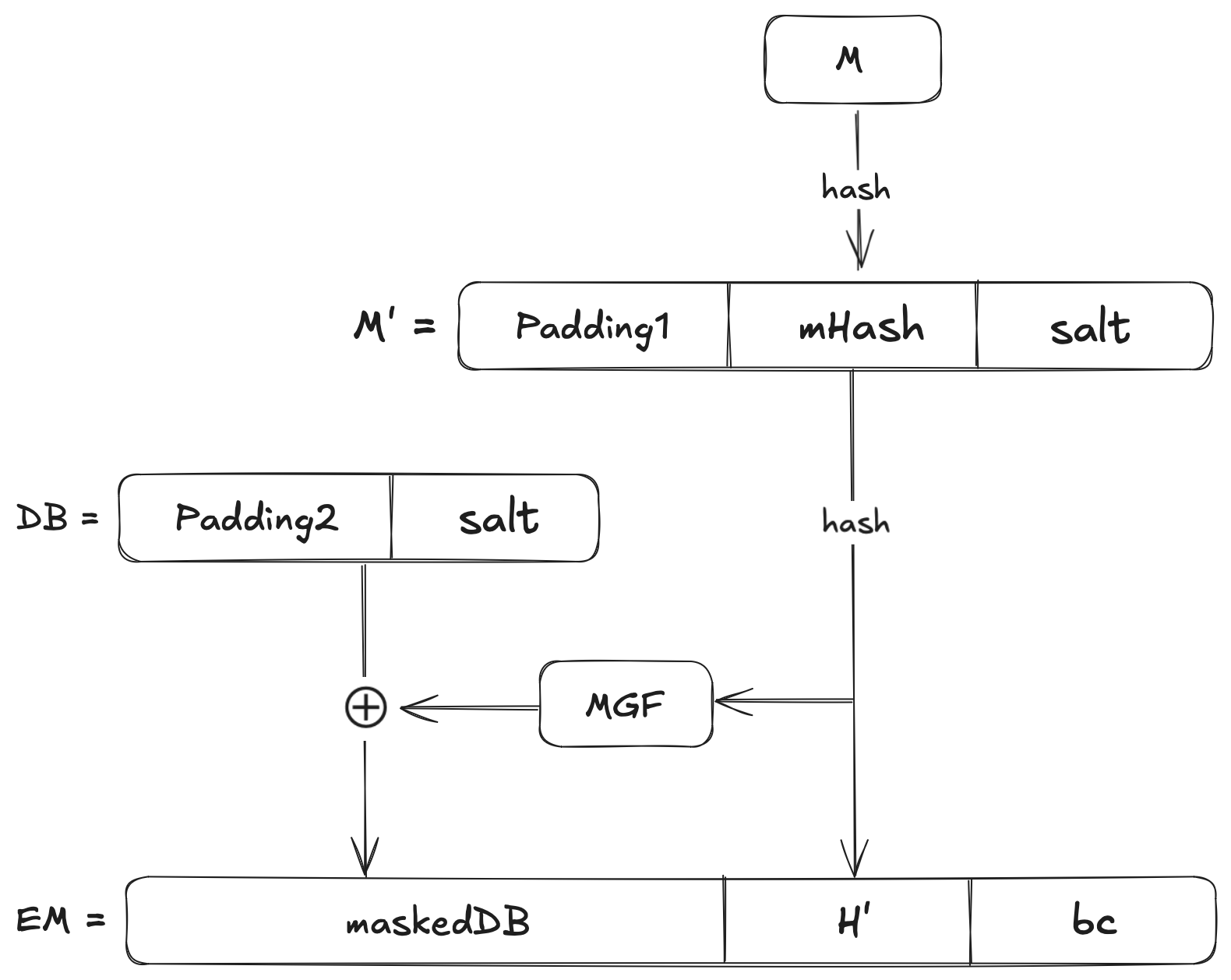
Let’s understand what these mathematical notions mean as well as the workings of RSA-PSS, up next.

The Mathematics Behind PSS

Before diving into the mechanics of RSA-PSS, it’s helpful to define the notations and terms you’ll see in the steps ahead.

In RSA, $N$ is the modulus, a large integer that is the product of two primes. $k$ is the length of $N$ in bytes. For an 2048-bit key, $k=256$ bytes.

$M$ represents the message data or document you want to sign. In RSA-PSS, you’ll typically first compute a hash of $M$ . Hash refers to a cryptographic hash function (for example, SHA-256) that maps data to a fixed-size output. The output length is denoted $hLen$ . For SHA-256, $hLen=32\:\text{bytes}$ .

We will use a salt, $S$ , randomly generated string of fixed length (often the same as $hLen$ ). This randomness is essential in ensuring that each signature is unique, even for the same message.

$H$ or $mHash$ is the hash of the message $M$ and $H'$ is a secondary hash that includes both $M$ and the salt $S$ . This appears in the PSS encoding step.

The Mask Generation Function, $MGF$ , is a function that uses the hash internally to produce a pseudorandom output of arbitrary length. In PSS, it is used to “mask” parts of the data block so that the signature is hard to forge.

A fixed byte, $0\text{x}bc$ (in hex) is appended at the end of the encoded message to mark the boundary of the PSS structure. This serves as a simple integrity check during decoding. After a successful encoding we receive an encoded message $EM$ which is an octet string of length $emLen=\left\lceil\tfrac{emBits}{8}\right\rceil$ .

Now that you are familiar with all the necessary notations, we are ready to begin the encoding step.

Step 1: Message Hashing and Salt Generation

We compute the hash of the message as $H\left(mHash\right)=Hash\left(M\right)$ where $M$ is our message. We will also create a random salt $S$ (of fixed length, say 20 bytes if you use SHA-1).

Step 2: Encoding the Hash with the Salt (PSS-Encode)

We will construct a Data Block, $DB$ , by combining a padding with the hash and the salt. The padding is a sequence of $0$ ’s that fills space and ensures a fixed length. Mathematically:

M'=\left(0\text{x}\right)\:00\:00\:00\:00\:00\:00\:00\:00\:\vert\vert\:mHash\:\vert\vert\:salt

Now we compute the Hash of this block as $H'=Hash\left(M'\right)$ . We will generate another octet string $PS$ and concatenate it with the salt and $0\text{x}01$ as a delimiter:

DB=PS\:\vert\vert\:0\text{x}01\:\vert\vert\:salt

Note that $DB$ is an octet string of length $emLen−hLen−1$ . The mask that you see in the visual representation above must be of this length. Mathematically:

dbMask=MGF\left(H,\:emLen−hLen−1\right)

We will then apply this mask on the $DB$ block using an $XOR$ operation to produce our maskedDB:

maskedDB=DB\oplus{dbMask}

Recollect that $emLen$ is the intended length of the Encoded Message $EM$ and hLen is the length of the hash output. Now we append a fixed trailer field $0\text{x}bc$ and produce the encoded message in its octet string representation:

EM=maskedDB\:\vert\vert\:H\:\vert\vert\:0\text{x}bc

This encoding process ensures that both the salt and the hash are mixed together in a non-reversible, pseudorandom manner. The randomness from the salt is “spread” over the data block by the $MGF$ , making it extremely difficult for any adversary to manipulate the signature.

Step 3: RSA Signature Generation

Once you have the encoded message $EM$ , the RSA signature is produced by using the RSA private key. First, convert the Octet String to its integer representation using the OS2IP method we’ve discussed before. Then apply the RSA Private Key Operation:

s=m^{d}\:\text{mod}\:N

where $d$ is the private exponent and $N$ is the RSA modulus.

Step 4: Signature Verification

At the receiver end, when any recipient wants to verify a signature, they reverse the process:

m'=s^{e}\text{mod}\:N

Probabilistic signature scheme ↩︎
RFC 8017: RSASSA-PSS ↩︎