Exploiting Textbook RSA’s Determinism and Malleability

Hamdaan AliApril 3, 2025About 4 min

Exploiting Textbook RSA’s Determinism and Malleability 관련

The Cryptography Handbook: Exploring RSA PKCSv1.5, OAEP, and PSS

The RSA algorithm was introduced in 1978 in the seminal paper, ”A Method for Obtaining Digital Signatures and Public-Key Cryptosystems”. Over the decades, as RSA became integral to secure communications, various vulnerabilities and attacks have emerg...

The Cryptography Handbook: Exploring RSA PKCSv1.5, OAEP, and PSS

Key Generation (Setup)

For our toy example, we’ll choose small prime numbers and generate an RSA key pair:

Let’s select the values of $p=3$ and $q=11$ . Both of these values are prime. Now, compute the modulus and Totient Function as follows:

\begin{align*} n&=p\times{q}&=3\times{11}&=33\\ \phi\left(n\right)&=\left(p-1\right)\times\left(q-1\right)&=2\times{10}&=20 \end{align*}

Now choose the public exponent. Let’s consider $e=3$ since it is coprime with $\phi\left(n\right)=20$ , and $\text{gcd}\left(3,20\right)=1$ . Now let’s compute the private exponent. We know that $d$ is the modular inverse of $e\:\text{mod}\:\phi\left(n\right)$ . We need to find $d$ such that $\left(d\times{e}\right)\equiv{1}\left(\text{mod}\:20\right)$ . Using this knowledge we can compute $d=7$ as $3\times{7}=21\equiv1\:\left(\text{mod}\:20\right)$ .

Finally, the public key is ( $n=33$ , $e=3$ ) and the private key (secret) is $d=7$ .

Encryption Process

Now, let’s encrypt a simple message using the above key. Let us select our plaintext to be $M=4$ . The cipher text in this case would be:

\begin{align*} C&=43\:\text{mod}\:33\\ C&=64\:\text{mod}\:33\\ C&=64-33\times{1}&=31 \end{align*}

To consolidate the findings so far, if we encrypt message $4$ with the public key $(e=3,\:n=33)$ , we will produce the cipher text $31$ . Now, let’s try the exploits.

Determinism Exploit (Ciphertext Guessing Attack)

Textbook RSA is deterministic - the same plaintext always yields the same ciphertext (with no randomness involved). An attacker who intercepts the ciphertext $C=31$ can exploit this by encrypting likely plaintext guesses and comparing results:

The adversary, say Eve, will try encrypting candidate plaintexts with the public key and see which one produces $31$ . They may pick randomized values to increase their efficiency:

\begin{align*} \text{Guess}&\:M=1&\Rightarrow\:13\:\text{mod}\:33&=1\\ \text{Guess}&\:M=2&\Rightarrow\:23\:\text{mod}\:33&=8\\ \text{Guess}&\:M=3&\Rightarrow\:33\:\text{mod}\:33&=27\\ \text{Guess}&\:M=4&\Rightarrow\:43\:\text{mod}\:33&=31 \end{align*}

By simply comparing ciphertexts, the attacker finds that encrypting $4$ yields $31$ , which matches the intercepted ciphertext. Thus, the attacker learns the original plaintext $M$ was $4$ . This is possible because there’s no randomization in textbook RSA - an eavesdropper can identify a message by trial encryption of guesses, breaking confidentiality if the message space is small or guessable.

Malleability Exploit (Ciphertext Manipulation Attack)

Raw RSA is also malleable. This means an attacker can take a ciphertext and modify it in a way that results in a predictable change in the decrypted plaintext. Let’s understand how this works.

RSA has a multiplicative property, that is, multiplying two ciphertexts corresponds to multiplying their plaintexts before encryption:

\begin{align*} &E\left(M_{1}\right)\cdot{E}\left(M-{2}\right)\text{mod}\:n\\ =&\left(M-{1}^{e}\:\text{mod}\:n\right)\times\left(M_{2}^{e}\:\text{mod}\:n\right)\:\text{mod}\:n\\ =&\left(M_{1}\cdot{M}_{2}\right)\:e\:\text{mod}\:n \end{align*}

The sequence diagram below explains how the malleability exploit works in naive RSA.

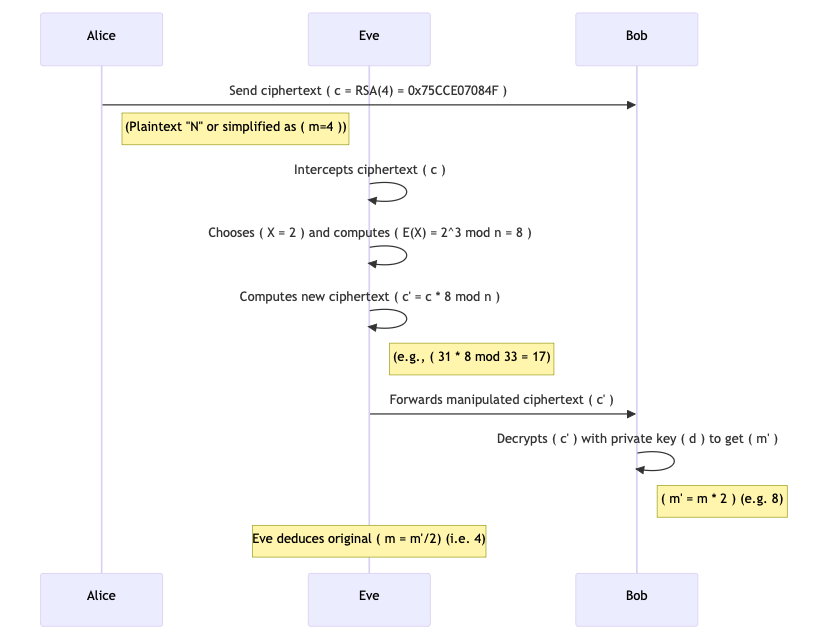
Alice sends a ciphertext to Bob after the initialization phase. Note that by this point, $n$ and $e$ are public knowledge. Eve intercepts this ciphertext by using mechanisms such as a MiTM (Man in the Middle) attack.

Now, Eve picks a known value to manipulate the message. Let’s say the attacker chooses $X=2$ (with the intent to double the original plaintext).

Then they compute the encryption of $X$ using the public key:

E\left(X\right)=2^{3}\:\text{mod}\:33=8

Now, Eve multiplies the original ciphertext by this value ( $\text{mod}\:n$ ) to get a new ciphertext:

\begin{align*} C'&=C\times{E}\left(X\right)\:\text{mod}\:n&=31\times{8}\:\text{mod}\:33\\ C'&=248\:\text{mod}\:33&=248-33\times{7}&=248-231&=17\\ \end{align*}

This new ciphertext $C'$ is the encryption of the product of the original plaintext and $2$ . If we directly encrypted $M\times{X}=4\times{2}=8$ with RSA, we would get $8^{3}\:\text{mod}\:33=512\:\text{mod}\:33=17$ . This means that $C'$ corresponds to the plaintext $8$ , which is the original message $4$ multiplied by $2$ .

In a real-world chosen ciphertext attack, the attacker may have access to a decryption oracle or observe a system response that reveals information about $M'$ . The decryption result 8 is exactly $M\times{2}$ (the original message multiplied by the attacker’s chosen factor). Knowing the factor $X=2$ , the attacker can deduce the original message by dividing: $\tfrac{8}{2}=4$ . Note that Eve has not broken the mathematical foundations behind RSA here. They have only used the public key to compute an encryption of $2$ , and then combined it with the intercepted ciphertext. They don’t know the original plaintext yet, but they have manipulated the ciphertext in a way that they know the new plaintext is twice the original message.