Public Key Cryptography Standards (PKCS#1 v1.5)

Hamdaan AliApril 3, 2025About 5 min

Public Key Cryptography Standards (PKCS#1 v1.5) 관련

The Cryptography Handbook: Exploring RSA PKCSv1.5, OAEP, and PSS

The RSA algorithm was introduced in 1978 in the seminal paper, ”A Method for Obtaining Digital Signatures and Public-Key Cryptosystems”. Over the decades, as RSA became integral to secure communications, various vulnerabilities and attacks have emerg...

The Cryptography Handbook: Exploring RSA PKCSv1.5, OAEP, and PSS

In 1998, Kaliski and RSA Laboratories introduced PKCS#1 v1.5 to the world in a public publication^[1]. In PKCS#1 v1.5, every RSA‐encrypted message is wrapped inside a special “encryption block” $EB$ . This block ensures that the raw message is both the right size for RSA and padded in a way that’s hard to tamper with.

In this scheme, the plaintext is padded to the size of the modulus $N$ (in bytes) as:

EB=00\:\vert\vert\:BT\:\vert\vert\:PS\:\vert\vert\:00\:\vert\vert\:M

Here, $0\text{x}00$ (Leading Zero Byte) is always at the front. It ensures that, when the concatenated string $EB$ is converted to a big‐endian integer, the value is less than the RSA modulus (that is, we don’t end up with a number too large for RSA to handle). You will better appreciate this fact when we dive into the mathematics behind this.

The next octet is the Block Type, $BT$ , which tells us the “type” of padding being used. The standard defines three possible $BT$ values: $00$ , $01$ , and $02$ - to support different operations. For example, $BT=00$ and $BT=01$ is used for private-key operations (such as digital signatures) and $BT=02$ is used for public-key operations. For encryption under PKCS#1 v1.5, this is always 0x02. It’s basically a label that says, “This is an encryption block, not something else”.

The next block is the Padding String $PS$ . This is a string of nonzero random bytes. This is crucial for security because it introduces randomness into each encryption. If the same message is encrypted multiple times, these random bytes ensure that each ciphertext looks different, foiling many simple attacks that rely on seeing repeated patterns.

The next octet, $0\text{x}00$ , is a Delimiter. This single zero byte marks the end of the padding. During decryption, this helps the recipient quickly identify where the padding stops and the real message begins.

Finally, we have the actual data you want to protect – $M$ . Once the recipient has verified the padding, they know exactly where to find this message.

This mechanism helped solve the deterministic issue of naive RSA. In the next sections, let’s understand the mathematics involved in PKCS#1 v1.5 padding and its security implications.

The Mathematics Behind PKCS#1 v1.5

Before we begin, let’s get our symbols and abbreviations correct. We will use upper-case symbols (such as $EB$ ) to denote octet strings and bit strings. We will use lower-case symbols (such as $n$ ) to denote integers.

In PKCS#1 v1.5, we will use k to represents the length of the RSA modulus $n$ in bytes. For example, if you have a 1024-bit RSA key, then the RSA modulus n is a 1024-bit number. Since there are 8 bits in a byte, if your RSA modulus is L bits long, then:

k=\left\lceil\frac{L}{8}\right\rceil=\frac{1024}{8}=128\:\text{bytes}

The total length of the encryption block will be equal to this RSA key length $k$ (in bytes). Now here the length of the data M shall not be more than k−11 octets, since the $11$ bytes are consumed by the blocks – $0\text{x}00\:\vert\vert\:0\text{x}02\:\vert\vert\:PS\:\vert\vert\:0\text{x}00$ . This limitation guarantees that the length of the padding string $PS$ is at least eight octets, which is a security condition in PKCS#1v1.5:

\vert{PS}\vert=k-\vert{M}\vert-3

For example, with a 1024-bit RSA modulus, the value of $k$ comes out to be $128$ . Here Alice could encrypt up to $128−11=117$ bytes of data. The $11$ bytes are used for the $0\text{x}00\:\vert\vert\:0\text{x}02\:\vert\vert\:PS\:\vert\vert\:0\text{x}00$ structure. The random $PS$ ensures that each encryption of the same message produces a different ciphertext, preventing the deterministic encryption problem.

RSA doesn’t directly operate on the bytes. Once the padded string $\text{EB}$ is ready, it needs to be converted into an integer guided by the Octet String to Integer Primitive (OS2IP) formula:

x=\sum_{i=1}^{k}2^{8\left(k−i\right)}\text{EB}_{i}

where $\text{EB}_{i}$ are the octets of $EB$ from first to last. In other words, $\text{EB}_{1}$ (the first byte) is the most significant byte, and $\text{EB}_{k}$ (the last byte) is the least significant. Now Alice can simply encrypt this block using $C=x^{c}\:\text{mod}\:n$ .

To solidify our learnings so far, let’s apply this to a sample plaintext and find the padded blocks.

Let’s assume the RSA modulus is 8 bytes long $(k=8)$ . Suppose we want to encrypt a message $M$ that is $2$ bytes long. Then the padding string $PS$ must fill the remaining space:

\begin{align*} \text{Total bytes}&=k=8=1\left(0\text{x}00\right)+1\left(BT\right)+\left\vert{PS}\right\vert+1\left(\text{delimiter}\right)+\left\vert{M}\right\vert \end{align*}

Since $\left\vert{M}\right\vert=2$ and there are $\left\vert{M}\right\vert=2$ fixed bytes, can find the required length of the padding string:

\left\vert{PS}\right\vert=8−3−2=3\:\text{bytes}

Let’s pick 3 arbitrary nonzero bytes for $PS$ , say - $0\text{x}A3$ , $0\text{x}5F$ , $0\text{x}C2$ . And let’s say the message is the ASCII text “Hi”. In hexadecimal, that’s: $0\text{x}48$ for ' $H$ ' and $0\text{x}69$ for ' $i$ '.

Thus, the complete encryption block becomes:

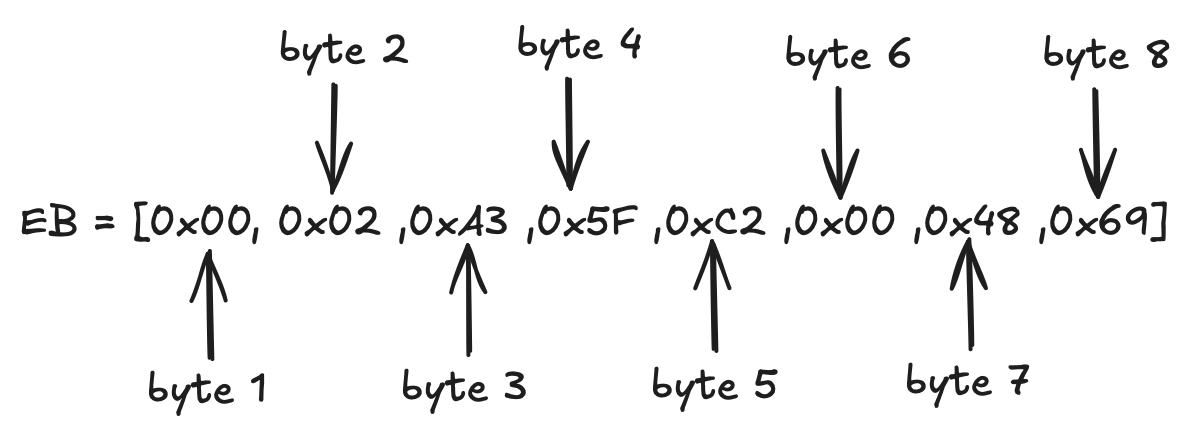
Now we will convert this octet string to an integer using the OS2IP formula we discussed above:

x=\sum_{i=1}^{k}2^{8\left(k−i\right)}\text{EB}_{i}

For our example, with $k=8$ the conversion is:

\begin{align*} x&=0\text{x}00\times{256}^{7}\\ &+0\text{x}02\times{256}^{6}\\ &+0\text{x}A3\times{256}^{5}\\ &+0\text{x}5F\times{256}^{4}\\ &+0\text{x}C2\times{256}^{3}\\ &+0\text{x}00\times{256}^{2}\\ &+0\text{x}48\times{256}^{1}\\ &+0\text{x}69\times{256}^{0} \end{align*}

Note that the hexadecimal values can be converted to decimal as needed. For instance, $0\text{x}A3=163$ , $0\text{x}5F=95$ , $0\text{x}C2=194$ , $0\text{x}48=72$ , and $0\text{x}69=105$ . There is an interesting observation in the application of this formula. Because the first two bytes are fixed ( $0\text{x}00$ and $0\text{x}02$ ), the integer x has a known lower bound. The contribution of the first two bytes is:

0\times{256}^{7}+2\times{256}^{6}=2\times{256}^{6}

The rest of the bytes ( $PS$ , the delimiter, and $M$ ) add some value that is at least $0$ and at most just less than $256^{6}$ (since the second byte is fixed as $0\text{x}02$ and cannot be $0\text{x}03$ ). Thus, $x$ is in the range:

2\times{256}^{6}\le{x}\lt{3}\times{256}^{6}

This property which makes the range predictable, paved the way for the Bleichenbacher attack (also known as the “padding oracle” attack). If a system reveals whether a decrypted block is “correctly padded,” an attacker can systematically probe different ciphertexts and narrow down the plaintext – because the attacker knows it must lie in that narrow range. Let’s take a detailed look at the Bleichenbacher attack in the next sections and understand how the exploit works.

RFC 2313: PKCS #1: RSA Encryption ↩︎