Optimal Asymmetric Encryption Padding (OAEP)

Hamdaan AliApril 3, 2025About 5 min

Optimal Asymmetric Encryption Padding (OAEP) 관련

The Cryptography Handbook: Exploring RSA PKCSv1.5, OAEP, and PSS

The RSA algorithm was introduced in 1978 in the seminal paper, ”A Method for Obtaining Digital Signatures and Public-Key Cryptosystems”. Over the decades, as RSA became integral to secure communications, various vulnerabilities and attacks have emerg...

The Cryptography Handbook: Exploring RSA PKCSv1.5, OAEP, and PSS

By the end of 1995, Bellare and Rogaway proposed Optimal Asymmetric Encryption Padding (OAEP) with the goal of achieving provable security. This padding aimed to make RSA encryption resistant not just to passive attacks but also to adaptive chosen-ciphertext attacks. In other words, even if an attacker can trick a system into decrypting chosen ciphertexts (as an “oracle”), they should learn nothing useful about the plaintext. OAEP was subsequently standardized in PKCS#1 v2.0 (published as RFC 2437 in 1998) and later versions.

Compared to PKCS#1 v1.5, OAEP has a more complex encoding that uses hash functions and a mask generation function (MGF) to thoroughly randomize the plaintext before RSA encryption, providing stronger guarantees.

OAEP’s design can be viewed as a two-layer Feistel-like network using a random seed. It takes the input message and randomizes it in a way that is reversible only with the correct seed. The scheme was proven plaintext-aware in the random oracle model which means that an adversary cannot concoct a valid ciphertext without knowing the corresponding plaintext. If an attacker tries to forge or tamper with ciphertexts, they almost surely produce an invalid padding that will be rejected. This property directly counters padding-oracle attacks.

OAEP (with a proper hash/MGF) is semantically secure against adaptive chosen ciphertext attacks, assuming RSA is hard to invert and treating the hash functions as random oracles. Unlike PKCS#1 v1.5, which lacked a formal proof, OAEP comes with a proof sketch that breaking RSA-OAEP is as hard as breaking RSA itself.

In practice, this means OAEP drastically reduces the risk of any padding oracle: an attacker can no longer easily find ciphertexts that slip through the padding check except by brute force which has a $2^{-hLen\times{8}}$ success probability. For example, the success probability with SHA-1 would be $2^{−160}$ . The block diagram below is a visual representation of the OAEP encoding schema:

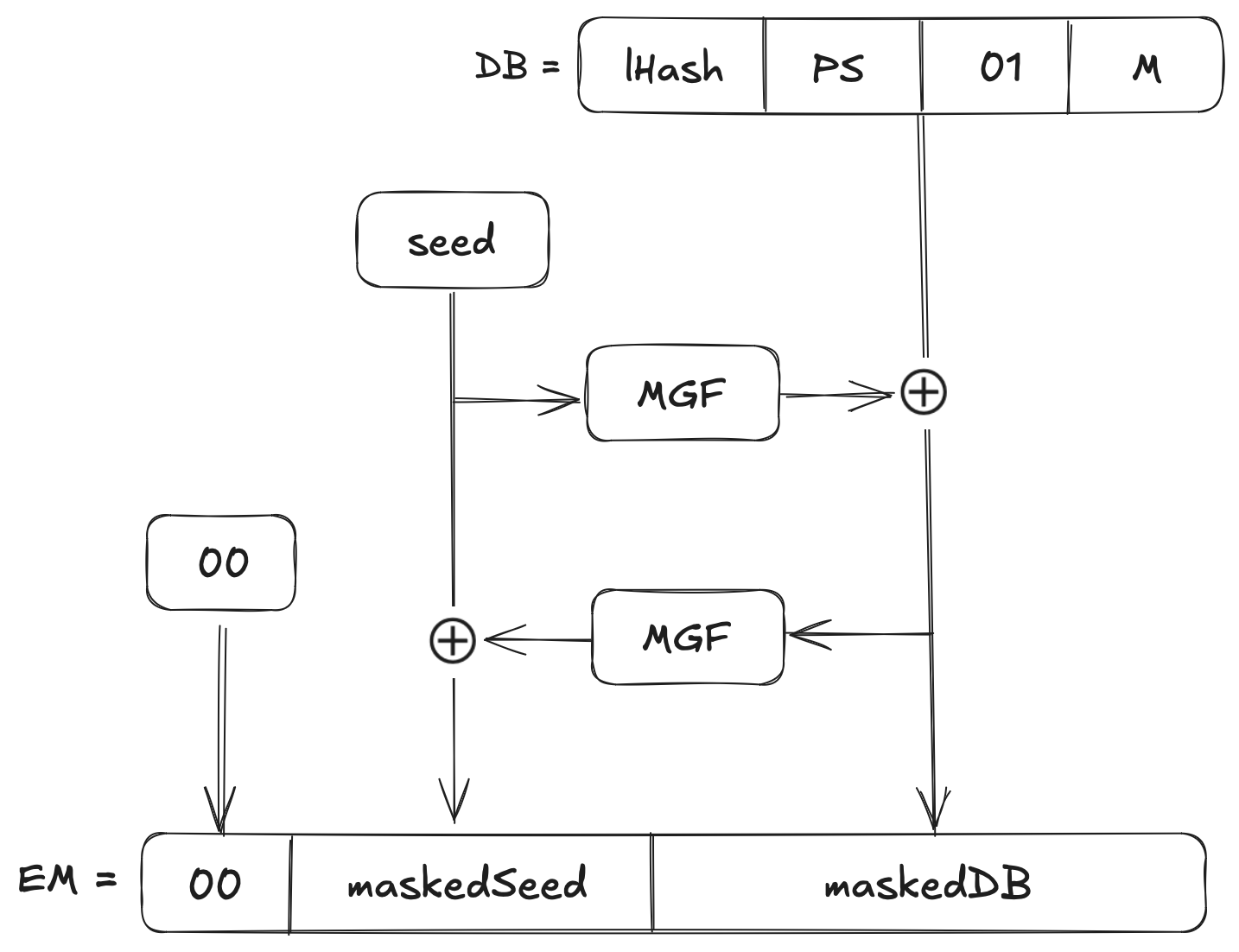
Let’s understand what these mathematical notions mean and the workings of RSA-OEAP, up next.

The Mathematics Behind OAEP

Optimal Asymmetric Encryption Padding requires a hash function for two operations we will discuss in this section. We will choose SHA-1 as a hash function in OAEP and $hLen$ denotes the length in octets of the hash function output. We will later demonstrate why even MD5 or SHA-1 is a secure choice for OAEP even if it is not collision resistant.

Before we dive into the mathematics, let’s recap a few notations and define the main pieces we’ll be using:

In RSA, $N$ is the modulus, and $k$ is the size of $N$ in bytes. For a 2048-bit modulus, $k=256$ bytes.

$M$ is the message or plaintext to be encrypted. This plaintext must be short enough to fit into the padded block (at most $k−2\cdot{hLen}−2\:\text{bytes}$ ). In our notation, Hash refers to the cryptographic hash function (for example, SHA-1, SHA-256) of output length hLen. For example: If using SHA-1, $hLen=20\:\text{bytes}$ .

We will also use an optional string associated with the message (often empty). This is the Label $L$ . If this label is empty, its hash is a fixed value. (For example: the SHA-1 of an empty string).

The hash of this label L is represented by $lHash$ , where $lHash=Hash\left(L\right)$ . As mentioned earlier, if $L$ is empty, $lHash$ is simply $Hash\left(^{''}\right)$ . This means that in any case $lHash$ will hold a value.

We will also use a Mask Generation Function, $MGF$ , which is often mentioned as $MGF1$ . This function takes an input (seed or masked data) and produces an output of a specified length by iterating the underlying hash function. We’ll write $MGF\left(input,length\right)$ to indicate “generate a mask of length bytes from input”.

Now that you are familiar with all the necessary notations, we are ready to begin the encoding step.

Step 1: Constructing the Data Block (DB)

We will compute $lHash=Hash\left(L\right)$ . If $L$ is empty, $lHash$ is a constant (For example, the SHA-1 of the empty string).

Form the padding string $PS$ , the length of $PS$ is chosen so that the entire block $DB$ has length $(k−hLen−1)\:\text{bytes}$ . Numerically, $PS$ has $\left(k−mLen−2\cdot{hLen}−2\right)$ bytes of $0\text{x}00$ , where $mLen$ is the length of the message $M$ .

Now we simply concatenate the blocks to generate the octet string for the Data Block ( $DB$ ):

DB=lHash\:\vert\vert\:PS\:\vert\vert\:0\text{x}01\:\vert\vert\:M

Here the single byte $0\text{x}01$ acts as a delimiter which marks where the zero padding ends and the actual message $M$ begins. $DB$ ends up being $\left(k−hLen−1\right)\:\text{bytes}$ .

Step 2: Generating a Mask for the Data Block

First, we pick a random string called seed of length $hLen$ bytes. For example, when using SHA-1 where $hLen=20$ , then we say that the seed consists of $20$ random bytes.

Now we use the mask generation function, $MGF$ , on the seed to create a mask the same length as $DB$ :

dbMask=MGF\left(seed,\:k−hLen−1\right)

The idea is to spread the randomness of the seed across the entire $DB$ .

Step 3: Mask the Data Block

Now, we will Combine $DB$ and $dbMask$ with the bitwise $XOR$ operation:

maskedDB=DB\oplus{dbMask}

This step “scrambles” $DB$ with the random seed.

Step 4: Generate a Mask for the Seed

Next, we will produce a mask for the seed itself, based on $maskedDB$ :

seedMask=MGF\left(maskedDB,\:hLen\right)

This step simply ensures that the seed is not left in the clear.

Step 5: Mask the Seed

Now we will combine the original seed and the new mask with an $XOR$ operation:

maskedSeed=seed\oplus{seedMask}

Now the seed is also “scrambled” by the data block.

Step 6: Form the Final Encoded Message ( $EM$ )

We are now ready to build our final block. Simply concatenate everything into a k-byte string:

EM=0\text{x}00\:\vert\vert\:maskedSeed\:\vert\vert\:maskedDB

The leading $0\text{x}00$ byte ensures that when $EM$ is interpreted as an integer, it’s less than the RSA modulus $N$ . At this point, $EM$ is your OAEP-padded message of length $k$ .

Step 7: Covert concatenated String to Integer

Remember from our discussion before on PKCS#1v1.5 that RSA cannot directly operate on this concatenated string of bytes. We need to convert the $EM$ block to a non-negative integer using the OS2IP formula:

x=\sum_{i=1}^{k}2^{8\left(k−i\right)}\text{EB}_{i}

Step 8: Perform RSA Encryption

Now that we have the encoded message ( $EM$ ) as an integer $x$ , we are ready to perform RSA guided by the formula:

C=x^{e}\:\text{mod}\:N

where $\left(e,N\right)$ is the public key. The thus computed $C$ is our ciphertext generated using RSA-OAEP.

When decrypting, the process is reversed: the recipient uses their private key $d$ to compute $m=c^{d}\:\text{mod}\:N$ , recovers the $EM$ , then splits it into the $0\text{x}00$ , $maskedSeed$ , and $maskedDB$ , and uses the same $MGF$ and hash function to unravel the $XOR$ s in reverse order. Finally, they check that the recovered $lHash'$ matches the expected hash and that the block contains the proper structure $\left(\dots\:\vert\vert\:0\text{x}01\:\vert\vert\:\dots\right)$ .

If any check fails, the padding is invalid. Only if everything checks out is the message M returned. The result is that an invalid ciphertext will almost always be detected and rejected without giving an attacker any useful information.

By design, OAEP effectively foiled the padding oracle problem. The chance that a random guess produces a valid OAEP encoding is negligible (on the order of $2−hLen\times8$ ). In fact, Daniel Bleichenbacher (after breaking PKCS#1 v1.5) advocated for exactly such a “plaintext-aware” padding where forging a valid padding is infeasible.