The Bleichenbacher Attack

Hamdaan AliApril 3, 2025About 4 min

The Bleichenbacher Attack 관련

The Cryptography Handbook: Exploring RSA PKCSv1.5, OAEP, and PSS

The RSA algorithm was introduced in 1978 in the seminal paper, ”A Method for Obtaining Digital Signatures and Public-Key Cryptosystems”. Over the decades, as RSA became integral to secure communications, various vulnerabilities and attacks have emerg...

The Cryptography Handbook: Exploring RSA PKCSv1.5, OAEP, and PSS

In 1998, Daniel Bleichenbacher published a seminal paper[^8] demonstrating an adaptive chosen-ciphertext attack against RSA with PKCS#1 v1.5 padding. The Bleichenbacher Attack, also dubbed as the “million messages” attack, demonstrated that if an attacker has access to an oracle that tells whether a submitted ciphertext decrypts to a properly padded plaintext (that is, whether the PKCS#1 v1.5 formatting is correct), the attacker can gradually recover the full plaintext. Let’s break down how this attack works:

First, Eve needs an Oracle. The attack assumes the attacker can query a system, such as an SSL/TLS server, and find out if a given ciphertext $C$ is PKCS#1 v1.5 conformant. In the 1998 paper, Bleichenbacher exploited the fact that a TLS server, when presented with an improperly padded RSA-encrypted premaster secret, would respond with a specific error alert if the padding was wrong. Essentially, the server acted as an oracle: it would decrypt $C$ with its private key and simply tell the attacker “padding OK” or “padding error” (the error could be timing-based or an explicit alert).

Note that the oracle does not reveal the plaintext. It only reveals a single bit of information at a time: “valid padding or not.” This might seem harmless, but Bleichenbacher showed that it’s enough to eventually recover the plaintext.

To quickly recap, the attacker’s goal is to find the unknown message integer $m$ (the PKCS#1-padded plaintext as an integer) given its ciphertext $C=m^{e}\:\text{mod}\:N$ , using the oracle. We know that if $m$ is properly padded, it lies in a specific numeric range: $2B\le{m}\lt{3B}$ where $B=2^{8\times\left(k−2\right)}$ , as defined earlier.

If $k=128\:\text{bytes}$ , then $B=2^{8\times{126}}$ , and a correctly padded $m$ will start with $0\text{x}00\:\vert\vert\:0\text{x}02$ , so it’s between $2B$ and $3B$ . The attacker, Eve, initially only knows that $m$ is in the range $\left[2B,3B\right)$ .

In the Bleichenbacher Attack, Eve will exploit RSA’s multiplicative property. They will choose a number $s$ (called the multiplier) and compute a new ciphertext $C'=\left(Cs^{e}\right)\:\text{mod}\:N$ . This $C'$ here corresponds to a new plaintext: $m'=ms\:\text{mod}\:N$ (because $C'\equiv{m}^{e}\times{s}^{e}\equiv\left(ms\right)^{e}\:\left(\text{mod}\:N\right)$ ).

To begin the attack, Eve finds some $s_{0}$ such that $C_{0}=C\times\left(s_{0}\right)^{e}\:\text{mod}\:N$ yields a valid padding. This is referred to as the Blinding step. This is usually easy – for example, $s_{0}$ can be chosen so that $m\times{s}_{0}$ is just slightly above $N$ , which almost certainly will wrap around and land in $\left[2B,3B\right)$ . The attacker does not know m to verify this directly. They rely on the padding oracle’s yes/no response to infer that the blinded plaintext $\left(m\times{s}_{0}\right)\:\text{mod}\:N$ falls in the correct range.

If the oracle returns “valid padding” for a given $s_{0}$ , it tells the attacker that $s_{0}\:\text{mod}\:N$ lies between $2B$ and $3B$ . Mathematically:

2B\le\left(m\times{s}_{0}\right)\:mod\:N\lt{3B}

Now, Eve will try to try to narrow down this range in a loop, which is often referred to as the interval having step. Initially, Eve had one wide interval $\left[a,b\right]=\left[2B,3B\right)$ that contains $m$ . In each iteration, Eve tries increasing values of $s$ (starting from a certain minimum) until the oracle returns “padding OK” for $C'=C_{0}\times{s}^{e}$ . Suppose this happens at some $s=s_{i}$ . Given this feedback, Eve now knows:

2B\le\left(𝑚\times{s}_{i}\right)\:\text{mod}\:N\lt{3B}

This congruence implies there exists some integer $r$ such that:

2B\le\left(m\times{s}_{i}\right)−rN\lt{3B}

Rearranging, we get a constraint on $m$ :

\frac{2B+rN}{s_{i}}\le{m}\lt\frac{3B+rN}{s_{i}}

Eve doesn’t know $r$ outright, but they can solve for the possible range of $r$ by considering the current interval $\left[a,b\right]$ for m. Essentially, Eve uses the previous bounds on $m$ to guess which $r$ would make the inequality true, then updates the new bounds $\left[a,b\right]$ as the intersection of all possible solutions for $m$ . This dramatically shrinks the interval.

Each oracle query yields such a constraint. Eventually, the interval $\left[a,b\right]$ collapses to a single value, $\left[a,a\right]$ . Now, Eve can find the plaintext using:

m=\left(a\times{s}_{i}^{−1}\right)\:text{mod}\:N

At that point, Eve has recovered the entire padded plaintext $m$ , and by stripping off the padding, the original message itself.

The sequence diagram below consolidates our learning of the attack:

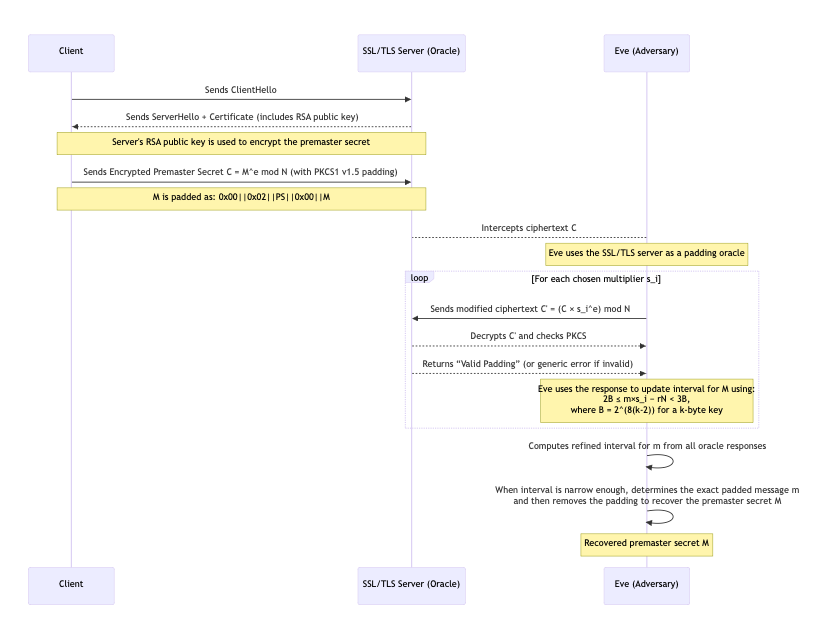
Sequence Diagram: The Bleichenbacher’s Attack

The Bleichenbacher attack showed that the format of the padding in PKCS#1 v1.5 leaked just enough info to enable a full private-key operation (decrypting the message) without ever factoring $N$ . The attack leveraged the fact that it’s possible to craft ciphertexts that will decrypt to a valid-looking plaintext without knowing the plaintext. In essence, PKCS#1 v1.5 padding allowed about $1$ in $2^{16}$ chance (roughly) for a random blob to appear as “valid padding.” That was enough for an adaptive attack to succeed with feasible queries.

This is precisely what later padding designs like OAEP fixed. OAEP’s design makes such random valid ciphertexts astronomically unlikely (plaintext aware). We will learn about RSA-OAEP in the next sections.

To mitigate the Bleichenbacher attack without immediately changing the padding scheme, practitioners implemented defensive measures. For example, TLS should treat all decryption failures the same way (so an attacker can’t distinguish padding vs. other errors), and servers would generate a fake premaster secret on padding failure to continue the handshake and avoid timing leaks. Nonetheless, the safest course has been to deprecate PKCS#1 v1.5 encryption in favor of schemes like RSA-OAEP.