
How Does Recursion Work? Explained with Code Examples
How Does Recursion Work? Explained with Code Examples 관련

In this article, you will learn about recursion and how it works.
You need a good understanding of how functions work before learning recursion. I have used Python code for examples in this article because of its simple syntax, but the concept of recursion is the same for every programming language.
What is Recursion?
In most programming languages, a function can call another function. But a function can also call itself. Recursion is the technique where a function calls itself.
Here's an example:
def call_me():
call_me()
Here, the function calls itself, which is called recursion.
But "calling itself" is just a programmatic definition of recursion. Recursion involves breaking down a problem into smaller pieces to the point that it cannot be further broken down. You solve the small pieces and put them together to solve the overall problem.
Real Life Analogy of Recursion
Lets understand how recursion really works with the help of an example.
Imagine you're in line for a Disney ride, and you don't know how many people are ahead of you.
To find out, you ask the person in front of you.

That person also doesn't know, so they ask the person in front of them.
This process continues until the question reaches the person at the very front of the line, who sees that there is no one in front of them and replies that there are zero people ahead.
The replies then start to propagate back through the line. Each person adds one to the number they were told before passing the information back.
When the person at the front replies, "There are 0 people ahead" the next person adds one and replies, "There is 1 person ahead" and so on.

By the time the response reaches the person directly in front of you, they add one more and tell you. This way, you can determine your position in the line by just adding 1 to the number the person in front of you gave.
This example illustrates how recursion breaks a problem into smaller subproblems and then combines their solutions to solve the original problem.
Each person in the line represents a smaller instance of the same problem: determining the number of people ahead. By solving these smaller instances and combining their results, the overall problem is resolved. This is exactly how recursion works.
Technical Details of Recursion
The most important things to consider while coding recursion is to find out:
- Recursive Case: Minimum work we can do. In the above example, asking the person in front of you how many people are ahead of them is the least amount of work we can do.
- Base Case: Condition where no work is required. In the above example, the person on the front of the line doesn’t have to ask anything so it is the condition where no work is required.
Simple Example of Recursion
Calculating a factorial is the simplest example of recursion that will really help you understand how it works.
There are many ways to calculate the factorial of a number. But here we will see the recursive way to find it.
Before thinking about how we do it, we need to know what the factorial of a number is.
The factorial of a number is the multiplication of all numbers from up to that number.
For example, the factorial of is - that is .
We can also represent this mathematically like this:
This means that if we know the value of we can easily get the factorial by just multiplying by it.
Here’s how we find the factorials of , , , , and :
Factorial of 4 = 4×(4−1)!
Factorial of 3 = 3×(3−1)!
Factorial of 2 = 2×(2−1)!
Factorial of 1 = 1
Factorial of 0 = 1
By looking at this, it is clear that to find the factorial of , we must multiply by .
More general example
To find the factorial of , we need to multiply with . This is something you need to do recursively.
Now, there must be a stopping condition for recursion. The stopping condition is where we perform no further operation. When is or is , we can simply stop the recursion as these values have known factorials. We can simply say the factorial of is and the same is true for
So, breaking it down, the minimum amount of work we need to do to find the factorial of n is . And we can stop performing operations on it when we find the factorial of or .
Let's see how it looks in code:
# calculate factorial of n
def fact(n):
# no work required
if n == 1 or n == 0:
return 1
# minimum amount of work
return n * fact(n - 1)
n = 5
# calculate factorial
factorial = fact(n)
print(factorial)
#
# Output:
#
# 120
Let's see how it works:
In the first function call, the factorial of is evaluated. Then in the second call, the factorial of is evaluated, and so on until the factorial of is evaluated.

While calling the factorial of , we have 2×fact(2−1), which is 2×fact(1).
This hits our base case. So, the recursion stops and 2×fact(1) returns 2×1 to the preceding function call, and the result gets popped up the stack.

Similarly, here’s how everything else evaluates:
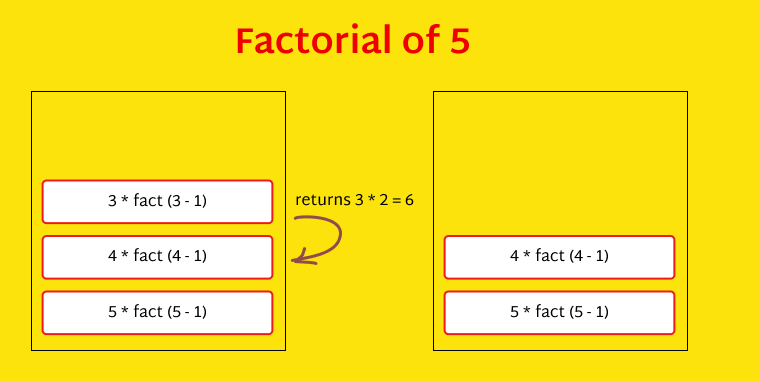
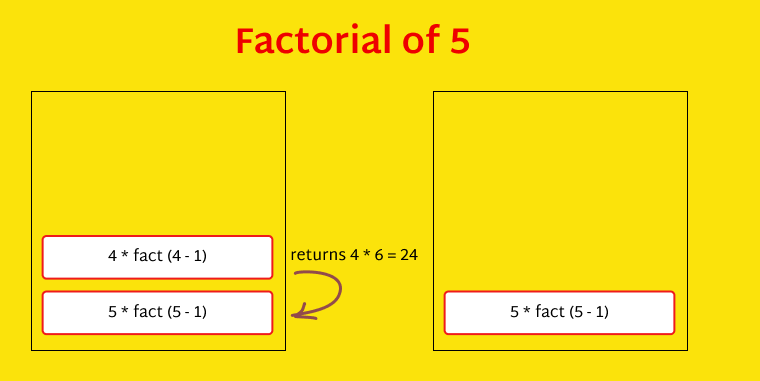

So the function finally returns the value to the initial function call.
Why Do We Need a Base Case?
In the above example we have used the stopping condition for the code. But what if we don’t add a stopping condition or what if the function we write never meets the stopping condition?
Will the code run forever?
No - even if you don’t terminate, your code won't run forever. Let’s understand why this is the case with the help of an example.
def print_five():
print(5)
# call itself
print_five()
# function call
print_five()
#
# Output:
#
# 5
# 5
# 5
# ...
# RecursionError: maximum recursion depth exceeded
If you run the above code, you will see that the function doesn’t run forever and ends with a message RecursionError: maximum recursion depth exceeded.
When a function is invoked, it is stored in a call stack. Here's how the function print_five() is stored in the call stack when it is invoked for the first time.

The function calls itself again and again, and the function is stored in the call stack with each call.

But the call stack has a limited size and cannot store an unlimited number of functions.
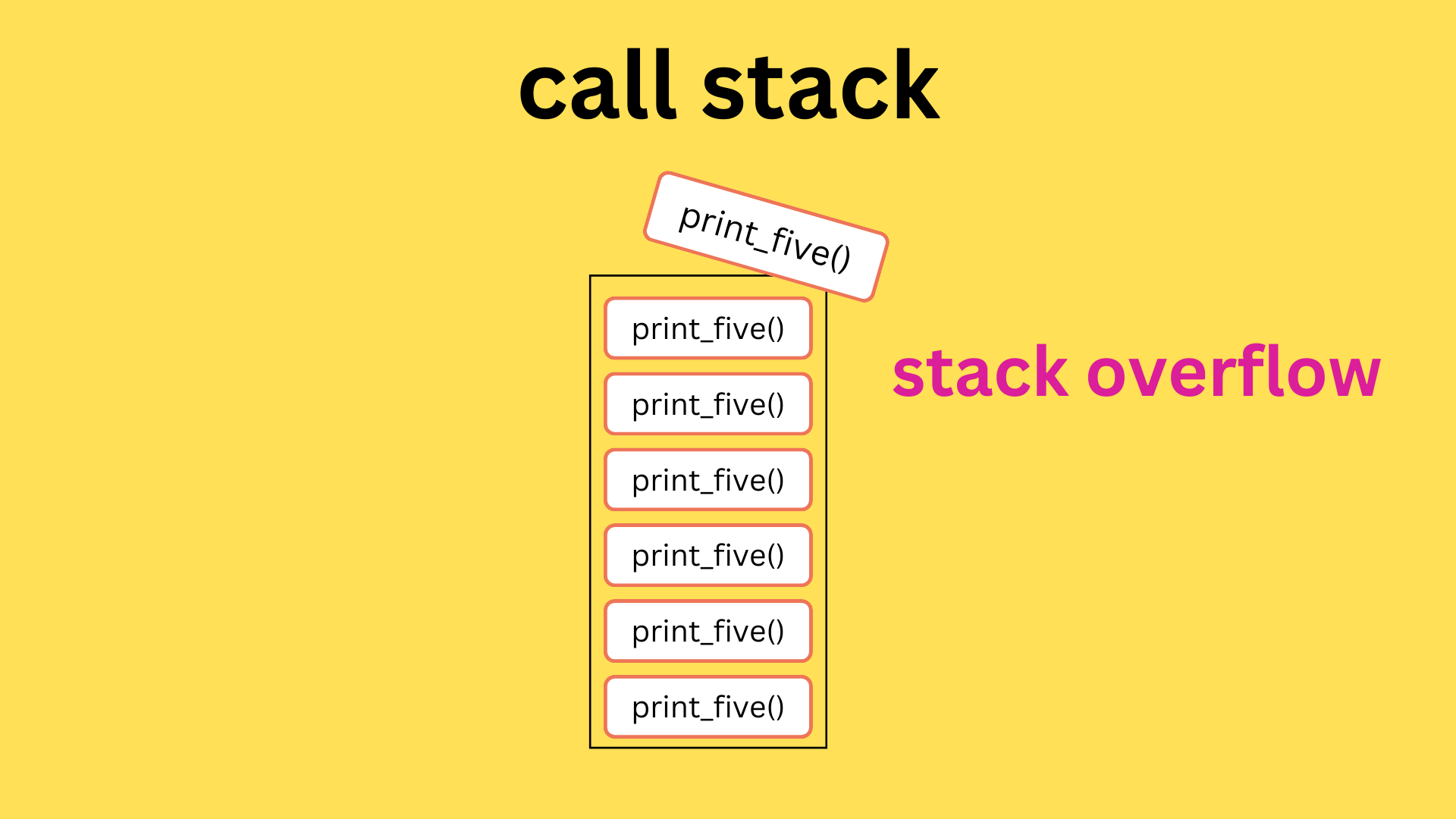
When the stack is full, it cannot accommodate any more calls, causing a stack overflow error.
Therefore, the base case is essential to prevent such errors and ensure the recursion terminates properly.
Now let's see another example to understand recursion even more.
How to Check if a Word is a Palindrome
Before we dive into the code, you should know what a palindrome is. A palindrome is a word that reads the same forwards and backwards.
For example, racecar reads the same forwards and backwards.
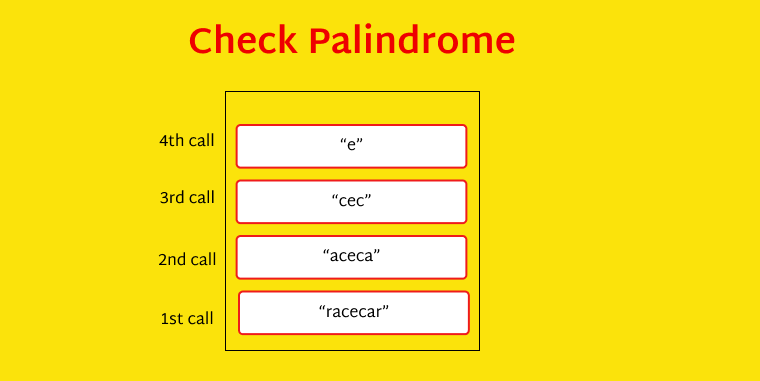
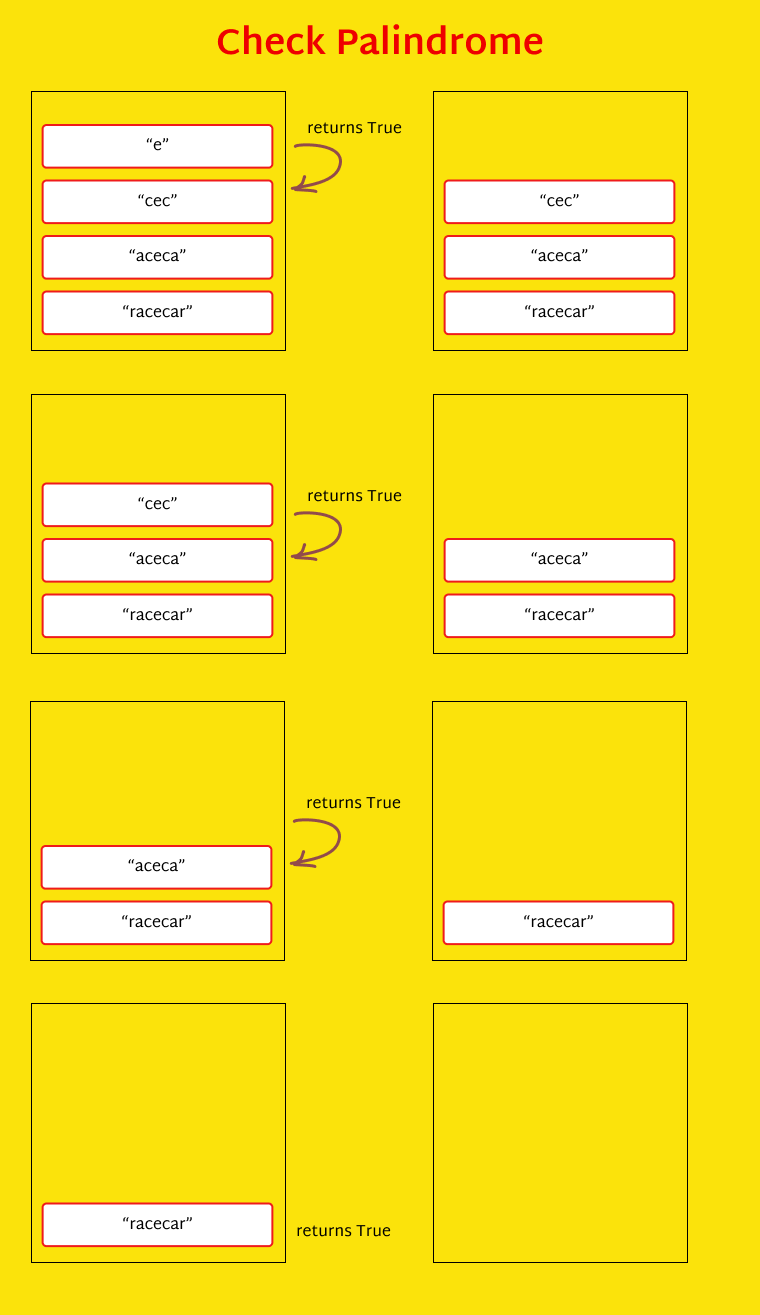
To check if a word is a palindrome, we have to check if the first and last letters are the same. If they are, we then check if the second and second-to-last letters are the same.

In the context of racecar, the first and last letters are the same, so we check if the second and second-to-last letters are the same. They are, so now we check if the third and third-to-last letters are the same. Now there is only one letter left to check. A single letter is always a palindrome because it reads the same both ways.
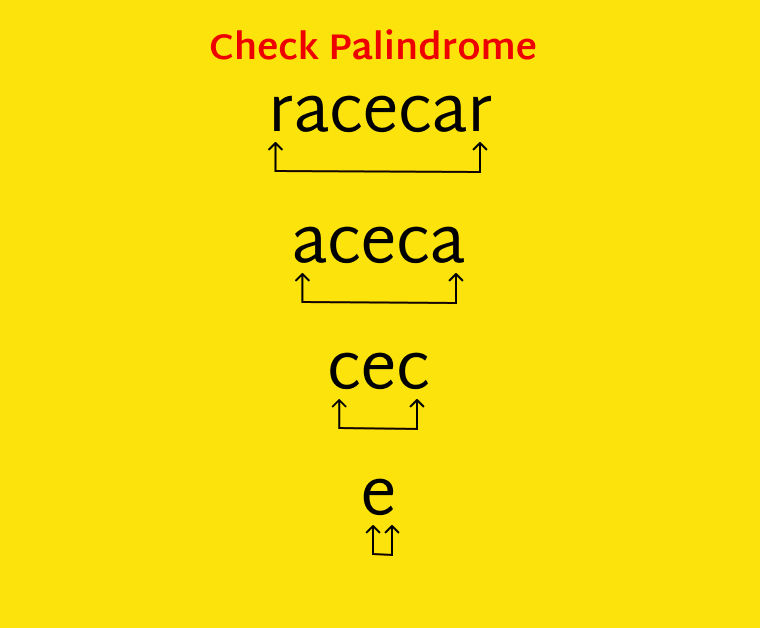
So, now let's try thinking about it recursively, which involves the minimum amount of work and determining when no work is required.
Minimum amount of work
Check if the first and last letters are the same, and if they are, remove the first and last letters from the word.
No work required
When there is one letter or no letters left at all, we can simply say it is a palindrome.
Now, let's see how the code looks:
# check palindrome
def check_palindrome(text):
# stopping condition
# if the size of text is 1 or 0 return true
if len(text) == 0 or len(text) == 1:
return True
# least amount of work
# check if first and last char are the same
# if same remove first and last char from string
if(text[0]==text[-1]):
return(check_palindrome(text[1:-1]))
return False
# check if string is palindrome
text = "racecar"
is_palindrome = check_palindrome(text)
print(is_palindrome)
Here's how the above code works:
When to Use Recursion
Recursion can appear elegant and simple. But it often requires many steps to solve even simple problems due to the CPU overhead from repeatedly adding methods to the stack. So before using it, make sure you carefully consider whether it's the right solution for your problem.
When code requires multiple loops and looks confusing and messy, recursion can offer a cleaner solution. Its use, however, depends on the specific code and the type of data or data structure involved. For data structures like trees and graphs, recursion can be particularly useful.
Despite its simplicity in appearance, recursion can be hard to understand and may take multiple steps even for simple problems. So again, make sure you think about your particular use case.
Wrapping Up
This is just an introduction to recursion. There are many cases where recursion is used, and you might be confused about how everything works. I will cover more advanced examples on recursion in the next article.
By the way, here are the resources that I found simple and useful while learning recursion:
- freeCodeCamp video on recursion: I have to give a shout-out to freeCodeCamp for their excellent video on recursion, which inspired much of this article.
- Recursion by Programiz Pro: Another good resource is the Recursion course by Programiz. It's a premium course, so it's not free, but it's thoughtfully designed. Plus, you can actually practice directly on their platform, which makes it well worth it.
No matter where you learn from, don't spend too much time searching for the perfect resource. Just grasp the concepts and start practicing—that's the only way you'll truly learn.